Numbrisüsteemid ja tingimused

Kolm peamist valdkonda, mis erinevad meie arvudest

Kujutage ette, kui palju lihtsam oleks esimestel aastatel aritmeetikat õppida, kui peaksite õppima ainult sellist joont nagu mina ja kolmnurka kirjutama. Seda pidid põhimõtteliselt tegema kõik Mesopotaamia iidsed inimesed, ehkki nad varieerisid neid siin ja seal, pikutades, keerates jne.

Neil polnud meie pliiatseid ja pliiatseid ega paberit. See, mille nad kirjutasid, oli tööriist, mida saaks kasutada skulptuuris, kuna meedium oli savi. See, kas seda on raskem või kergem õppida kui pliiatsit, on ju nuputamine, kuid siiani on nad lihtsuse osakonnas ees, kus on õppida ainult kaks põhisümbolit.

Järgmine samm viskab mutrivõtme lihtsuse osakonda. Me kasutame a

Filmis "Homoge to Babylonia" [Matemaatiline väljaanne, Vol. 76, nr 475, "Matemaatika ajaloo kasutamine matemaatika õpetamisel" (märts 1992), lk. 158-178], ütleb kirjanik-õpetaja Nick Mackinnon, et ta kasutab Babüloonia matemaatikat, et õpetada 13-aastastele lastele muid aluseid peale 10. Babüloonia süsteem kasutab base-60, mis tähendab, et kümnendkoha asemel on see seksimaalne.

Nii Babüloonia numbrisüsteem kui meie oma loodavad väärtuse andmise positsioonile. Kaks süsteemi teevad seda erinevalt, osaliselt seetõttu, et nende süsteemil puudus null. Babüloonia vasakult paremale (kõrgelt madalale) positsioneerimissüsteemi õppimine peamise aritmeetika esmaseks maitsmiseks pole tõenäoliselt enam on keeruline kui õppida meie kahesuunalist, kus peame meeles pidama komakohtade järjekorda - koma suurendades, neid, kümneid, sadu ja siis lehvitades teisel pool teisel poole, ei ole onssi kolonni, vaid kümnendikud, sajandikud, tuhandikud jne.

Tutvustan Babüloonia süsteemi seisukohtadega järgmistel lehekülgedel, kuid kõigepealt on mõned olulised arvsõnad, mida õppida.

Me räägime aastaperioodidest, kasutades kümnendsummasid. Meil on kümnend kümme aastat, sajand 100 aastat (10 aastakümmet) või 10X10 = 10 aastat ruudus ja millennium 1000 aastat (10 sajandit) või 10X100 = 10 aastat kuupmeetrites. Ma ei tea ühtki kõrgemat terminit, kuid need pole need üksused, mida babüloonlased kasutasid. Nick Mackinnon osutab Senkarehi (Larsa) tahvelarvutilt Sir Henry Rawlinsonilt (1810-1895) * ühikute kohta, mida babüloonlased kasutasid, mitte ainult asjassepuutuvate aastate jooksul, vaid ka eeldatavate koguste osas:

1. soss
2. närv
3. sar.

sossnersosssarsoss

Ikka pole lipsulõhkujat: ruut- ja kuupmeetriliste aastaterminite õppimine pole tingimata lihtsam ladina keeles kui see on ühesilbilised babüloonia keeled, mis ei hõlma kubistamist, vaid korrutamist 10.

Mida sa arvad? Kas numbri põhitõed oleks olnud raskem õppida Babüloonia koolilapsena või ingliskeelses koolis moodsa õpilasena?

* George Rawlinson (1812-1902), Henry vend, näitab lihtsustatud transkribeeritud ruutude tabelit Iidse idamaailma seitse suurt monarhiat. Tabel näib olevat astronoomiline ja põhineb Babüloonia aastate kategooriatel.

Kõik fotod pärinevad sellest George Rawlinsoni 19. sajandi väljaande veebiskannitud versioonist Iidse idamaailma seitse suurt monarhiat.

Kuna me kasvasime üles erineva süsteemiga, on Babüloonia numbrid segane.

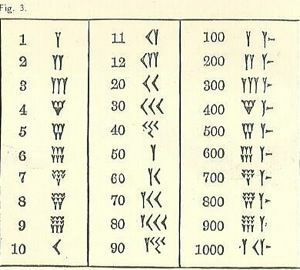
Vähemalt jooksevad numbrid kõrgelt vasakult madalalt paremale, nagu meie araabia süsteem, kuid ülejäänud tunduvad ilmselt harjumatud. Ühe sümbol on kiil või Y-kujuline. Kahjuks tähistab Y ka 50-d. Seal on mõned eraldi sümbolid (kõik põhinevad kiilul ja joonel), kuid kõik muud numbrid moodustatakse neist.

Pidage meeles, et kirjutamise vorm on cuneiform või kiilukujuline. Joonte joonistamiseks kasutatud tööriista tõttu on valik piiratud. Kiilul võib olla saba või mitte, see tõmmatakse hariliku kirjutuspliiatsi tõmbamisega mööda savi pärast osa kolmnurga vormi jäljendamist.

10, mida kirjeldatakse nooleotsana, näeb välja pisut nagu

Kolm rida, mis koosnevad kuni 3 väikesest 1-st (kirjutatud nagu Y-d mõne lühema sabaga) või 10-st (10 kirjutatakse nagu

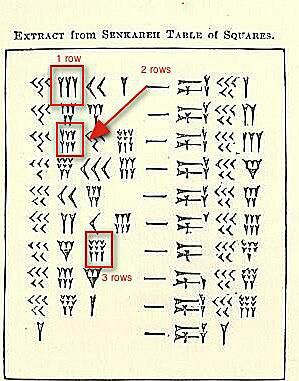
Hullu numbreid on kolm komplekti klastrid ülaltoodud joonisel esile tõstetud.

Praegu ei tegele me nende väärtusega, vaid sellega, kuidas näidata, kuidas näeksite (või kirjutaksite) kuskil 4–9 sama numbri rühmitatut. Kolm lähevad järjest. Kui on neljas, viies või kuues, läheb see allapoole. Kui seal on seitsmes, kaheksas või üheksas, vajate kolmandat rida.

Järgmistel lehekülgedel on juhised Babüloonia koopakujuliste arvutuste tegemiseks.

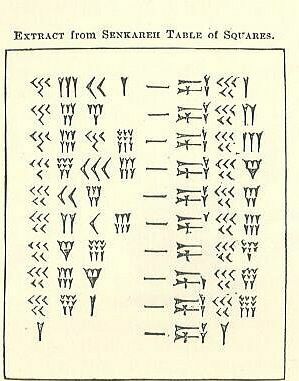
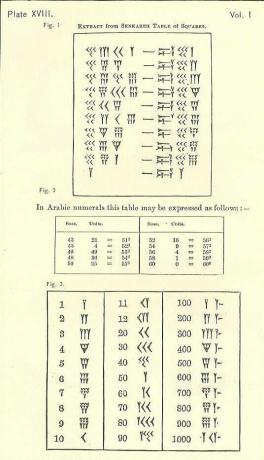
Sellest, mida olete eespool teemal lugenud soss - mis teile meelde tuleb, on Babüloonia 60 aastat, kiil ja noolepea - mis on müntmärkide kirjeldavad nimed, vaadake, kas saate aru, kuidas need arvutused töötavad. Kriipsutaolise märgi ühel küljel on number ja teisel ruut. Proovige seda rühmana. Kui te ei saa sellest aru, vaadake järgmist toimingut.

Kas saate seda nüüd välja mõelda? Andke sellele võimalus.

...

Vasakul küljel on 4 selget veergu, millele järgneb kriipsutaoline märk ja paremal 3 veergu. Vasakpoolsest küljest vaadates on 1s veeru ekvivalent tegelikult 2 kriipsule (sisesed veerud) lähimad veerud. Ülejäänud 2 välimist veergu arvestatakse 60-ndate veeruna.

• 4.
• 3-Y = 3.
• 40+3=43.
• Ainus probleem on siin see, et pärast neid on veel üks number. See tähendab, et nad ei ole üksused (nende oma). 43 ei ole mitte 43, vaid 43-60, kuna see on seksimaalne (baas-60) süsteem ja asub soss nagu alumine tabel näitab.
• Korruta 43 60-ga, et saada 2580.
• Lisage järgmine number (2 - 2
• Teil on nüüd 2601.
• See on 51 ruut.

Järgmisel real on 45 kohta soss veerus, nii et korrutate 45 60-ga (või 2700) ja lisate seejärel veerus ühikud 4, nii et teil on 2704. 2704 ruutjuur on 52.

Kas saate aru saada, miks viimane arv = 3600 (60 ruutu)? Vihje: miks pole see 3000?